GEOMETRÍA y TRIGONOMETRÍA
----- Grupo: 2° "A" Gericultura - 2º B Enfermería - . Período: Febrero - Junio 2023 -----
Hola ésta sección del Blog está dedicado a mis Alumnos de Geometría y Trigonometría
En este blog encontrarás todas las actividades que desarrollaremos en en semestre,
_______________ ********************* ________________
Actividades de ENCUADRE
Actividad 1.- Regístrate en el siguiente Formulario para Crear nuestra Lista de Asistencia:
Inicia Formulario...
Inicia Formulario
Finaliza Formulario...
Actividad 2.- Para estar comunicados...
- Da clic en Seguir para estar comunicados en Faccebook
| ||
Actividad 3.- Observa los siguientes Videos de Ayuda a tu Personalidad y Motivación:
Anota en tu Libreta tus Observaciones de los vídeos.
Actividad 4.- Documentos que debes Bajar:
- Debes Imprimir y Pegar en tu Libreta además de Firmarlo tú y tu Papá, Mamá o tu Tutor
|
Imprimir este Cuadro CQA, y sácale 5 copias, mantenlas disponibles, no las pegues.
|
Observa la Curricula de Materias que llevarás en tu Especialidad de Programación:
Actividad 5.- Anota el Programa de Estudios
Índice temático
Conceptos básicos del espacio y la forma
- Lección 1. El punto y la línea
- Lección 2. Trazo y clasificación de ángulos
- Lección 3. Suma y resta de ángulos (sistema sexagesimal)
- Lección 4. Clasificación de ángulos según su suma
- Lección 5. Conversiones de sistemas angulares
- Lección 6. Las figuras geométricas
- Lección 7. Elementos de las figuras geométricas
- Lección 8. Área y perímetro
- Lección 9. Teorema de Pitágoras
- Lección 10. Teorema de Tales
Cada lección se estructura por las siguientes secciones:
Propósito formativo del campo disciplinar de Matemáticas
Las competencias disciplinares básicas de Matemáticas buscan propiciar el desarrollo de la creatividad y el pensamiento lógico y crítico entre los estudiantes. Un estudiante que cuente con las competencias disciplinares de matemáticas puede argumentar y estructurar mejor sus ideas y razonamientos. Las competencias reconocen que a la solución de cada tipo de problema matemático corresponden diferentes conocimientos y habilidades, y el despliegue de diferentes valores y actitudes
Propósito de la asignatura
- Que el estudiante aprenda a identificar, analizar y comprender el uso de la configuración espacial y sus relaciones; así como, signifique las fórmulas de perímetro, área y suma de ángulos internos de polígonos.
- Que el estudiante aprenda a identificar, operar y representar el uso de los elementos figurales del ángulo, segmento, polígono, círculo y sus relaciones métricas.
De igual manera, se desarrollarán los Aprendizajes Clave de la asignatura de Geometría y Trigonometría:
- elementos básicos de Geometría.
- elementos de la Trigonometría plana.
Contenidos Centrales
- Conceptos básicos del espacio y la forma: “lo geométrico”.
- El estudio de las figuras geométricas y sus propiedades.
- Tratamiento de las fórmulas geométricas, los criterios de congruencia y semejanza de triángulos.
- Tratamiento visual de las propiedades geométricas, los criterios de congruencia y semejanza de triángulos.
- Conceptos básicos de lo trigonométrico.
- Usos y funciones de las relaciones trigonométricas en el triángulo. Funciones trigonométricas y sus propiedades.
Nuevo Modelo Educativo
Se incorporan las Habilidades socioemocionales (HSE) al Marco
Curricular Común en el Nuevo Modelo Educativo, lo cual, se concreta desde las asignaturas. Así, en
el caso de las asignaturas del segundo semestre, se promoverá el desarrollo de la Dimensión Conoce
T del Ámbito de Desarrollo Socioemocional.
Actividad 6.- Anota los Criterios de Evaluación
Aspecto
|
Actividades
|
Porcentaje
|
Total
|
Conceptual
|
Investigaciones / Tareas
|
10 %
|
10%
|
Procedimental
|
Examen Portafolio de evidencias Lecciones Edmodo / Blog Proyecto |
15%
10%
15%
10%
|
70%
|
Actitudinal
|
Asistencia
Conducta / Responsabilidad
Autoevaluación |
20%
|
|
TOTAL
|
100%
|
||
P R I M E R P A R C I A L
Actividades de APERTURA
Diagnóstico
Actividad 1.- Contesta el siguiente Formulario de Diagnóstico:
Inicia Formulario...
Inicia Formulario...
Fin Formulario...
Actividad 2.- Crea tu Blog o o Sitio Personal:
Crea tu Blog
1.- Uso de Blogs. Visualiza el Video Tutorial "Crea tu Propio Blog"
Si tienes problemas para verlo, prueba AQUÍ
o si gustas Crear tu Sitio en Google observa el siguiente Video Tutorial...
2.- Crea tu propio Blog anotando los puntos básicos mencionados en tu libreta.
- A continuación Crea una Entrada llamada Bienvenida en donde redactarás media cuartilla de Bienvenida mencionando a tus visitantes qué encontrarán en tu blog (unas 12 líneas).
- Crea una Página llamada Geometría y Trigonometría, por el momento vacía.
- Añade el Gadget Lista de Enlaces e Interrelaciona por lo menos 3 Blogs de tu compañeros del grupo, además añade mi enlace http://compendiodigitalpc.blogsppt.com como Profr. Baldo. Sigue las indicaciones del Video Tutorial creado por el Docente.
- El profesor te irá diciendo qué información vas a ir subiendo paulatinamente.
Una vez creado tu Blog debes dar tu Dirección URL al Profesor en el Formulario siguiente:
Inicia Formulario
- Crea tu Cuenta como Estudiante usando tu Correo de Gmail, o bien, si ya tienes cuenta en Edmodo, haz el paso siguiente.
- Ingresa al Grupo que te corresponde mediante el Código que se muestra:
GRUPO | Código | URL |
2º "B" Enfermería 2º "A" Gericultura | pendiente |
Realiza las Actividades 1 y 2 que se solicitan en Edmodo.
Actividad 4.- Utiliza 6 Hojas CQA. Imprímelas y pégalas en tu libreta, o bien, dibuja la Hoja CQA en tu libreta pero líneas bien hechas y escribe correctamente y legible.
La Primera con el Tema: ¿Qué es un Punto?
La Segunda con el Tema: ¿Qué es una Línea?
La Tercera con el Tema: ¿Qué es una Recta?
La Cuarta con el Tema: ¿Qué es un Segmento?
La Quinta con el Tema: ¿Qué es un Semirecta?
La Sexta con el Tema: ¿Qué es una Línea Curva?
De las 3 columnas que tiene la Hoja CQA,
- ¿Qué creo que es?,
- ¿Qué quiero aprender sobre el tema?,
- ¿Qué es?
Sigue las indicaciones del docente.
Por ejemplo, en la Columna 1 y 2 ¿Qué creo que es? y ¿Qué quiero aprender?... deberás anotar (sin hacer alguna investigación), lo que tú consideras que es, por ejemplo, el concepto de Algoritmo. Esto es, que al anotar en tus propias palabras lo que tú consideras que es un Algoritmo, estás indicando cuáles son tus conocimientos previos sobre el concepto. No te preocupes si tu concepto inicial no es el correcto, poco a poco captaremos el sentido y al final de la actividad tendrás certeza y habrás obtenido el aprendizaje esperado.
Por el momento NO debes llenar la columna 3. Debes llenar las Columnas 1 y 2 solamente en tus palabras.
Solo al final de la sesión, cuando el docente lo indique llenarás las Columna 3, la cual debe ser una Investigación del concepto obtenido de 2 fuentes diferentes.
Fin Sesión 2
Inicio Sesión 3
Actividades de DESARROLLO
Lección 1. El punto y la línea
Actividad 1.- 
Contesta las siguientes preguntas.
- ¿Qué ves a tu alrededor que no se relacione con alguna figura geométrica?
- ¿Qué figura geométrica no tiene líneas?
- ¿Qué tipos de líneas ves en las imágenes?
¿Cuántos tipos de línea existen?
Observa las imágenes ¿son líneas?
Actividad 2.- 
El punto
Concepto 1: Un punto se define desde el punto de vista geométrico y en un plano bidimensional como la unidad
más irreductiblemente mínima de la comunicación visual, es una figura geométrica sin dimensión,
tampoco tiene longitud, área, volumen, ni otro ángulo dimensional.
Concepto 2: El punto en Geometría se utiliza para indicar posición. La representación del punto es una
pequeña marca circular que se debe entender que no tiene dimensiones, es decir, no se puede medir.
Para identificar o denotar un punto se emplean letras mayúsculas. La siguiente figura muestra tres
puntos A, M y P
Tipos de línea
Una línea es una sucesión infinita de puntos sin separación entre ellos, lo que nos debe llevar a
aceptar que solo existen dos tipos de líneas:
la línea recta y
la línea curva.
- Recta Una recta es un conjunto sucesivo de puntos que se extienden infinitamente en ambos sentidos, tiene una sola dimensión (longitud). Para nombrar o denotar una recta se utilizan dos puntos cualesquiera que pertenezcan a ella con una flecha de doble punta sobre ellos o bien una letra minúscula, como se muestra a continuación: En la imagen encontramos la recta 𝐴⃡ 𝐵 (obsérvese que se dibuja una línea arriba de las letras) que pasa por los puntos A y B. La recta de la figura también está identificada como la recta r.
Cuando se habla de línea es común pensar en una línea recta pero ahora sabes que es un
error.
Todos los objetos del mundo real los podemos concebir, usando la
capacidad de abstracción, como formados por objetos geométricos; aunque
estrictamente hablando, no existen los objetos geométricos en el mundo real. Las
formas las podemos hacer reales si las despojamos de las características que no
son importantes para su estudio. Mediante la abstracción, podemos equiparar una
carretera con una recta o parte de esta, aunque sabemos que no solo tiene
longitud, un pizarrón con una porción de un plano, aunque no sea perfectamente
liso y así sucesivamente. Ejemplos:
Una característica de las líneas es que se pueden prolongar infinitamente.
No es posible y tampoco sería practico trabajar geométrica y/o matemáticamente con una
línea en su totalidad. Para cualquier análisis basta trabajar con una porción de ella y, de ahí se
desprende el concepto de segmento, el cual se define como la porción de una línea comprendida
entre dos puntos A y B (nótese el guion que se le debe de poner arriba de las letras mayúsculas). El segmento de recta anterior se denota 𝐴𝐵̅̅̅̅. La siguiente figura muestra el segmento de 𝐴𝐵̅̅̅̅ .
Si a una línea recta se le delimita solo un extremo a partir de un punto determinado se le llama
semirrecta.
Teniendo más de una recta en plano pueden darse unos casos particulares:
- que sean rectas paralelas
- que sean rectas perpendiculares o
- que sean rectas concurrentes de acuerdo con el ángulo que exista entre ellas.
Si consideramos un punto que divide a cualquier recta entonces esta se divide en dos porciones o partes. La porción que contiene al punto de división se le denomina rayo mientras que la parte que no contiene al punto, se llama semirrecta.
La notación del rayo y semirrecta se representan así:
Nota que el punto P está vacío, es decir, no pertenece a la semirrecta.
Plano Si una recta se traslada en una dirección distinta a la que se extiende, en ambos sentidos, barrerá una superficie, dicha superficie se conoce como Plano. Un plano tiene dos dimensiones de longitud. Un plano en matemáticas se imagina como una extensión ilimitada, ejemplo:
Una mesa de vidrio o la cubierta de un escritorio dan la idea de un plano, o más correctamente, porciones de un plano.
Un plano se representa geométricamente por una figura de cuatro lados y una letra mayúscula. La siguiente figura representa al plano P. También se puede nombrar utilizando 3 puntos que pertenezcan al plano. Por ejemplo, Plano ABC.
En un pizarrón se puede considerar el área verde como parte de un plano.
En la mesa de billar al espacio en morado es otro ejemplo de parte de
un plano.
Todos los objetos geométricos se pueden considerar compuestos de puntos, rectas y planos. Por ejemplo, los ángulos están formados por rayos, los cuales son, como ya sabes, porciones de rectas que quedan en un mismo plano.
Actividad 3.- 
Resuelve el crucigrama
Completa le siguiente texto.
Las ______________________ geométricas se encuentran representadas en todo nuestro entorno
son las que dan forma a nuestro mundo como lo conocemos. Muy en particular las líneas
_______________ se encuentra presente en la mayoría de los cuerpos, construcciones
y figuras geométricas regulares. Estas líneas y las líneas ______________________ al cruzarse
forman figuras y cuerpos geométricos de formas caprichosas y que se atraen la atención por no
tener formas cuadradas dado los ángulos que forman en la construcción de cuerpos y/o figuras no
son de 90°, como si sucede cuando las líneas se cruzan son ______________________ formando
de ángulos rectos lo que da formaciones cuadriláteras. Es increíble la cantidad de cuerpos y
figuras que podemos formas con tan solo líneas ____________, si a esto agregamos
que también contamos con las líneas __________________________ que provocan cambios en las
direcciones de los trazos; lo increíble se magnifica.
Actividad 4.- 
Actividad 5.- 
Te sugerimos consultar los siguientes recursos para facilitar tu práctica de asesoría
académica:
- Rubén Sebastián. ¿Qué es la línea? Línea recta y línea curva. YouTube [En línea] Disponible en: https://www.youtube.com/watch?v=MkCqQCeQsHs
- Ingeniat. Punto, Línea y Plano. YouTube [En línea] Disponible en: https://www.youtube.com/watch?v=_dMdsBRe9Ak
- Pensamiento geométrico grado 5°. [En línea] Disponible en: https://geometriaielp2010.blogspot.com/p/la-importancia-de-lageometria.html?m=1
- Krismar Education. Puntos, líneas y círculos imaginarios. YouTube [En línea]. Disponible en: https://www.youtube.com/watch?v=2wKsgM2QZfg
Fin Sesión 3
Inicio Sesión 4
Lección 2. Trazo y clasificación de ángulos
ACTIVIDADES DE APERTURA
Actividad 1.-
Contesta las preguntas y resuelve lo que se te pide.
¿Qué es un ángulo?
¿Cuántos tipos de ángulos conoces?
Remarca con diferentes colores los ángulos que observes en la imagen
Actividad 2.-
Tipos de ángulos según su medida
Un ángulo es la región del plano comprendida entre dos semirrectas con origen común. A las semirrectas se las llama lados y al origen común vértice.
Para medir ángulos utilizamos el grado sexagesimal (°). El grado sexagesimal es la amplitud del ángulo resultante de dividir la circunferencia en 360 partes iguales.
Los ángulos se miden en grados (°) y según su medida se clasifican en:
ACTIVIDADES DE DESARROLLO
Actividad 3.-
Traza los siguientes ángulos y escribe su nombre de acuerdo con su clasificación.
Actividad 4.-
Actividad 5.-
Te sugerimos consultar los siguientes recursos para facilitar tu práctica de asesoría académica:
- Daniel Carreón. Los de ángulos, súper fácil –Para principiantes. YouTube [En línea]. Disponible en: https://www.youtube.com/watch?v=-zLWJYY42GU
- Servicios educarm.es. Tipos de ángulos por tamaño [En línea]. Disponible en: http://servicios.educarm.es/alkaragi/content/contents/08/08c_04_b.htm
- Dibujar mejor. Como se usa el transportador y medir ángulos 29 de sep. YouTube [En línea]. Disponible en: https://www.youtube.com/watch?v=NtTOfe6vuQk
Fin Sesión 4
Inicio Sesión 5
Actividades de CIERRE
SEMANA DE EVALUACIÓN - EVIDENCIAS - EXAMENES PRIMER PARCIAL
Mantente Pendiente en CLASSROOM
de la Fecha de tu Examen
Héchenme ese Examen :)
Fin Sesión 5
Inicio Sesión 6
Actividad Complementa con este Recurso PDF los conceptos básicos sobre Ángulos. Imprime, pega y marca estos puntos. Si no puedes imprimir, entonces anótalo a mano en tu libreta.
Actividades de DESARROLLO
Lección 3. Suma y resta de ángulos (Sistema sexagesimal)
Actividad 1.-
Actividad 2.-
¿Qué unidad de medida utilizas para medir los ángulos?
Generalmente utilizamos el grado (°), el cual está presente en el transportador que es el instrumento con el que nos apoyamos para el trazo de estos. El grado es conocido como la medida angular o sistema sexagesimal. Sin embargo, para la suma y resta de ángulos se utilizan minutos (´) y segundos (´´), los cuales tienen la siguiente equivalencia:
Un grado equivale a 60 minutos. 1 ° = 60´
Un minuto es equivalente a 60 segundos. 1´= 60´´
Actividad Observa con atención el Video bajo el Tema Suma y Resta de Grados, Minutos y Segundos.
Toma notas en tu libreta..
Imagina que tienes una pizza y que cortas tres rebanadas:
- La primera es de 44° 10´ 60´´
- La segunda de 28° 42´
- La tercera de 34° 50´ 12´´
¿Cuánta pizza sobró?
Para dar solución a este problema tenemos que usar dos operaciones básicas suma y resta. Pero no es una suma cualquiera, los segundos no deben ser mayores a 60 y los minutos no deben exceder de los 59 (a menos que solo estés trabajando con grados y minutos estos pueden ser máximo de 60).
Ahora bien, la pizza tiene forma circular, es decir 360°. Esta cantidad la convertiremos a grados, minutos y segundos. Quedando de la siguiente manera:
A 360° le quite 1° que equivale a 60´´
360° = 359° 60´. Pero como también necesito segundos a 60’
le quite 1 minuto, ya que este equivale a 60 segundos.
Ahora realizaremos la resta
¿Qué sucede cuando los grados y minutos son menores los del minuendo?
Observa el siguiente ejemplo:
Actividad 3.-
Realiza las siguientes operaciones
Actividad 4.-
Actividad 5.-
Te sugerimos consultar los siguientes recursos para facilitar tu práctica de asesoría académica:
- AulaFacil. Suma y resta de ángulos. [En línea] Disponible en: https://www.aulafacil.com/cursos/matematicas-primaria/matematicas-sextoprimaria-11-anos/suma-y-resta-de-angulos-l7462
- Susi Profe. Suma de ángulos. YouTube. [En línea]. Disponible en: https://www.youtube.com/watch?v=hV7OWaKR1P0
- MClases. ¿Cómo restar ángulos con grados, minutos y segundos? YouTube [En línea] Disponible en: https://www.youtube.com/watch?v=8ydKdf7RX7w
Fin Sesión 6
Inicio Sesión 7
Regularización en Clases Presenciales
Fin Sesión 7
Inicio Sesión 8
Fin Sesión 8
Inicio Sesión 9
Regularización en Clases Presenciales
Grupo 2
Lección 4. Clasificación de ángulos según su suma
Actividad 1.-
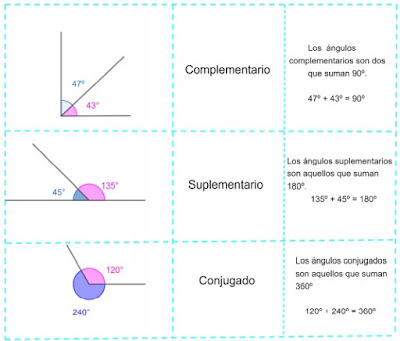
Coloca el nombre a cada uno de los siguientes ángulos
Actividad 2.-
Otra clasificación de los ángulos es por la suma de dos ángulos y tienen las siguientes
características:
Actividad 3 Observa con atención el Video bajo el Tema Tipos de Ángulos
Toma notas en tu libreta..
En este caso nos están pidiendo el valor del ángulo complementario 56° 36´ 28´´,
entonces, sabemos que los ángulos complementarios son aquellos que suman 90°, por lo
tanto, debemos restar a 90° el ángulo que conocemos, para ello debemos deshacer los 90°
en grado, minuto y segundo, quedando de la siguiente manera:
90° = 89° 59´ 60´´, en caso de que solo fueran grados y minutos quedaría 90°= 89° 60´
Una vez que tenemos las unidades necesarias podemos realizar la resta
El complemento de un ángulo de 56° 36´ 28´´ es uno ángulo 33° 23´ 32´´.
Comprobemos:
Actividad 4.-
Escribe los tipos de ángulos que observas en las imágenes
Calcula el valor del ángulo que falta
Actividad 4.-
Actividad 5.-
Te sugerimos consultar los siguientes recursos para facilitar tu práctica de asesoría
académica:
- José María Martín Rizaldos Ángulos complementarios y suplementarios, [En línea] Disponible en: https://www.youtube.com/watch?v=J3k7Qdv3Ylg.
- Educaplay. Ángulos complementarios, suplementarios y conjugados. [En línea] Disponible en: https://es.educaplay.com/recursos-educativos/2367910- angulos_complementarios_suplementarios_y_conjugados.html
- MateFacil. 09. Ángulos complementarios, suplementarios y conjugados ¿qué son? Y ejemplos. [En línea] Disponible en: https://www.youtube.com/watch?v=Nho8UZ1kgcQ
- AAAMath. Ángulos complementarios y suplementarios. 2004. [En línea] Disponible en: https://www.aaamatematicas.com/geo-comp-or-sup.htm
Fin Sesión 9
Lección 5. Conversión de sistemas angulares
Actividad 1.-
Contesta las siguientes preguntas.
- ¿Qué es ángulo?
- ¿Qué es radio?
- ¿Qué es pi?
- ¿Qué es circunferencia?
- ¿Qué es diámetro?
- ¿Qué es un radian?
- ¿Qué sistemas de unidades angulares existen?
Actividad 2.-
Importancia de los ángulos en la vida cotidiana
El estudio de los ángulos les permitió a los hombres abrirse paso en el mundo, edificando ciudades, construyendo herramientas y confeccionando su propia vestimenta, entre otras actividades. Todo esto a partir de la comprensión de importancia de aquel pequeño punto en que se interceptan dos rectas. El 100% de las cosas que rodean a la humanidad están hechas a partir de conocimientos geométricos y de trigonometría. Si bien, es cierto que la gran mayoría fueron automatizados por la industria y la tecnología, es bueno comprender cuál es la base de todo Podemos ver ángulos en casi cualquier parte de nuestro al rededor; por ejemplo, son usados para construir una casa como la que vemos en la imagen.
A continuación, te presentamos algunos conceptos básicos para la comprensión del tema:
Relación entre grados y radianes
Existen tres sistemas de medidas angulares: el sistema sexagesimal (conocido también como sistema ingles), el sistema centesimal (también conocido como sistema francés) y el sistema radial (también llamado sistema circular).
De los sistemas anteriores el sistema el más usado y conocido es sistema sexagesimal, sin embargo, el sistema radial es considerado un sistema más objetivo, por lo ello, es el sistema utilizado para fines matemáticos y el sistema de unidades angulares establecido por el sistema internacional de unidades (S.I.). Por ello, nos enfocaremos en esta lección en el sistema sexagesimal y el sistema radial.
El sistema Sexagesimal o inglés tiene como unidad al grado sexagesimal (1°) que es el resultado de dividir el ángulo de una vuelta en 360 partes iguales.
La vuelta completa de una circunferencia ha sido dividida en 360 partes iguales, entonces:
1 vuelta completa de una circunferencia = 360°
1° = 60’ = 3600”
1’ = 60”
El grado sexagesimal, también se divide en subunidades (Las subunidades se usan para expresar las medidas de ángulos menores a un grado)
Tenemos al minuto sexagesimal y al segundo sexagesimal
1´minuto sexagesimal
1´´ segundo sexagesimal
1° < > 60´
1´ < > 60´´
El sistema Radial o Internacional es aquel que tiene como unidad de medida a «un radian», definido como la medida de un ángulo central donde la longitud de arco que subtiende es igual al radio de la circunferencia que la contiene.
Estas equivalencias son la que permiten expresar una medida angular dada en grados (°) en términos de grados (°), minutos (’) y segundos (”) y viceversa.
Actividad 3.- Observa los siguientes Videos de Apoyo anotando en tu Libreta los Puntos Importantes y los Ejercicios mencionados.
Video 1 - Introducción
Video 2 - Introducción 2
Video 3 - Ejercicios
Fin Sesión 12